xarray¶
multi-dimensional data analysis in Python¶
ACINN workshop, Tue 07.02.2017
Fabien Maussion
Slides: http://fabienmaussion.info/acinn_xarray_workshop
Notebook: On GitHub
xarray¶
Documentation: http://xarray.pydata.org
Repository: https://github.com/pydata/xarray
Initial release: 03.05.2014
Latest release: v0.9.1 (20.01.2017)
53 contributors (latest release: 24)
Umbrellas: Python for data & NumFOCUS (but no funding...)
numpy.array¶
In [2]:
import numpy as np
a = np.array([[1, 3, 9], [2, 8, 4]])
a
Out[2]:
In [3]:
a[1, 2]
Out[3]:
In [4]:
a.mean(axis=0)
Out[4]:
xarray.DataArray¶
In [5]:
import xarray as xr
da = xr.DataArray(a, dims=['lat', 'lon'],
coords={'lon':[11, 12, 13], 'lat':[1, 2]})
da
Out[5]:
In [6]:
da.sel(lon=13, lat=2).values
Out[6]:
In [7]:
da.mean(dim='lat')
Out[7]:
xarray.Dataset¶
In [8]:
f = 'ERA-Int-MonthlyAvg-4D-TUVWZ.nc'
ds = xr.open_dataset(f)
ds
Out[8]:
Selection¶
By value¶
In [9]:
ds.t.sel(month=8, level=850)
Out[9]:
By index¶
In [10]:
ds.t.isel(month=7, level=11)
Out[10]:
By "wait... where is Innsbruck again?"¶
In [11]:
ds.t.sel(level=1001, latitude=47.26, longitude=11.38, method='nearest')
Out[11]:
The "old way"¶
In [12]:
ds.t[7, 11, :, :]
Out[12]:
Operations¶
Aggregation¶
In [13]:
ds.u.mean(dim=['month', 'longitude']).plot.contourf(levels=13)
plt.ylim([1000, 100]);
In [ ]:
And other kind of things¶
In [14]:
u_avg = ds.u.mean(dim=['month', 'longitude'])
u_avg_masked = u_avg.where(u_avg > 12)
u_avg_masked.plot.contourf(levels=13)
plt.ylim([1000, 100]);
In [ ]:
Arithmetic¶
Broadcasting¶
In [15]:
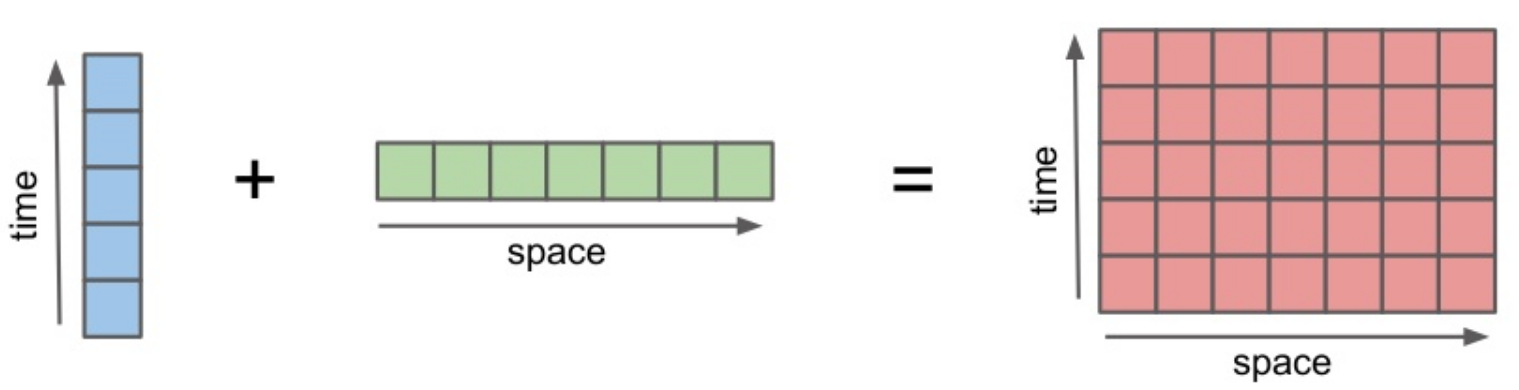
a = xr.DataArray(np.arange(3), dims='time',
coords={'time':np.arange(3)})
b = xr.DataArray(np.arange(4), dims='space',
coords={'space':np.arange(4)})
a + b
Out[15]:
Alignment¶
In [16]:
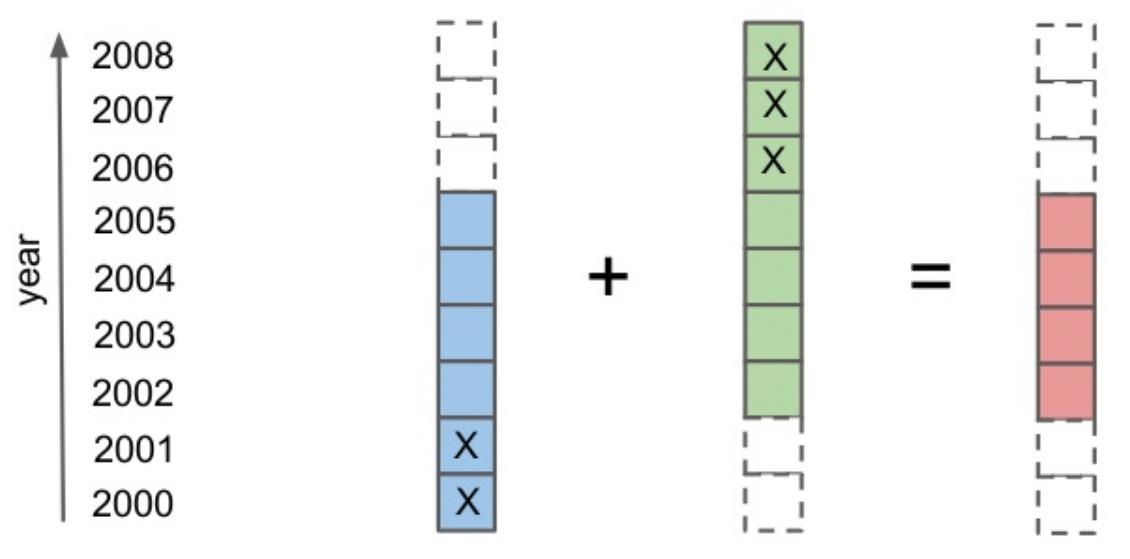
a = xr.DataArray(np.arange(3), dims='time',
coords={'time':np.arange(3)})
b = xr.DataArray(np.arange(5), dims='time',
coords={'time':np.arange(5)+1})
a + b
Out[16]:
Plotting¶
1-d¶
In [17]:
ts = ds.t.sel(level=1001, latitude=47.26, longitude=11.38, method='nearest')
ts.plot();
On maps¶
In [18]:
import cartopy.crs as ccrs
ax = plt.axes(projection=ccrs.Robinson())
ds.z.sel(level=1000, month=8).plot(ax=ax, transform=ccrs.PlateCarree());
ax.coastlines();
(Big) data: multiple files¶
Opening all files in a directory...
In [19]:
mfs = '/home/mowglie/disk/Data/Gridded/GPM/3BDAY_sorted/*.nc'
dsmf = xr.open_mfdataset(mfs)
... results in a consolidated dataset ...
In [20]:
dsmf
Out[20]:
... on which all usual operations can be applied:
In [21]:
dsmf = dsmf.sel(time='2015')
dsmf
Out[21]:
Yes, even computations!
In [22]:
ts = dsmf.precipitationCal.mean(dim=['lon', 'lat'])
ts
Out[22]:
Computations are done "lazily"
No actual computation has happened yet:
In [23]:
ts.data
Out[23]:
But they can be triggered:
In [24]:
ts = ts.load()
ts
Out[24]:
For more information: http://xarray.pydata.org/en/stable/dask.html
In [25]:
ts.plot();
ts.rolling(time=31, center=True).mean().plot();
Extensions¶
Example: EOFS¶
Taken from: http://ajdawson.github.io/eofs/examples/nao_xarray.html
In [26]:
from eofs.xarray import Eof
from eofs.examples import example_data_path
# Read geopotential height data using the xarray module
filename = example_data_path('hgt_djf.nc')
z_djf = xr.open_dataset(filename)['z']
# Compute anomalies by removing the time-mean.
z_djf = z_djf - z_djf.mean(dim='time')
# Create an EOF solver to do the EOF analysis.
coslat = np.cos(np.deg2rad(z_djf.coords['latitude'].values)).clip(0., 1.)
solver = Eof(z_djf, weights=np.sqrt(coslat)[..., np.newaxis])
# Get the leading EOF
eof1 = solver.eofsAsCovariance(neofs=1)
In [27]:
# Leading EOF expressed as covariance in the European/Atlantic domain
ax = plt.axes(projection=ccrs.Orthographic(central_longitude=-20, central_latitude=60))
ax.coastlines() ; ax.set_global()
eof1[0, 0].plot.contourf(ax=ax, levels=np.linspace(-75, 75, 11),
cmap=plt.cm.RdBu_r, add_colorbar=False,
transform=ccrs.PlateCarree())
ax.set_title('EOF1 expressed as covariance', fontsize=16);
Salem¶
- Adds geolocalized operations to xarray
- Adds projection transformations
- Adds WRF support
http://salem.readthedocs.io/en/latest/
Try it out:
pip install salemPlotting¶
In [28]:
# importing salem adds a new "toolbox" to xarray objects
import salem
In [29]:
pday = dsmf.precipitationCal.sel(time='2015-02-01')
cm = pday.salem.quick_map(cmap='Blues', vmax=100);
Subsetting¶
In [30]:
shdf = salem.read_shapefile(salem.get_demo_file('world_borders.shp'))
shdf = shdf.loc[shdf['CNTRY_NAME'].isin(['Peru'])]
In [31]:
dsmfperu = dsmf.salem.subset(shape=shdf, margin=10)
In [32]:
pday = dsmfperu.precipitationCal.sel(time='2015-02-01')
cm = pday.salem.quick_map(cmap='Blues', vmax=100);
Regions of interest¶
In [33]:
dsmfperu = dsmfperu.salem.roi(shape=shdf)
In [34]:
pday = dsmfperu.precipitationCal.sel(time='2015-02-01')
cm = pday.salem.quick_map(cmap='Blues', vmax=100);
... all xarray operations continue to apply¶
In [35]:
prpc_a = dsmfperu.precipitationCal.sum(dim=['time']).load()
In [36]:
prpc_a.salem.quick_map(cmap='Blues', vmax=5000);