Advanced programming: performance#
The rules of optimization#
Don’t do it.
(For experts only) Don’t do it yet.
Inspired from famous internet programmer knowledge.
Rules of thumb#
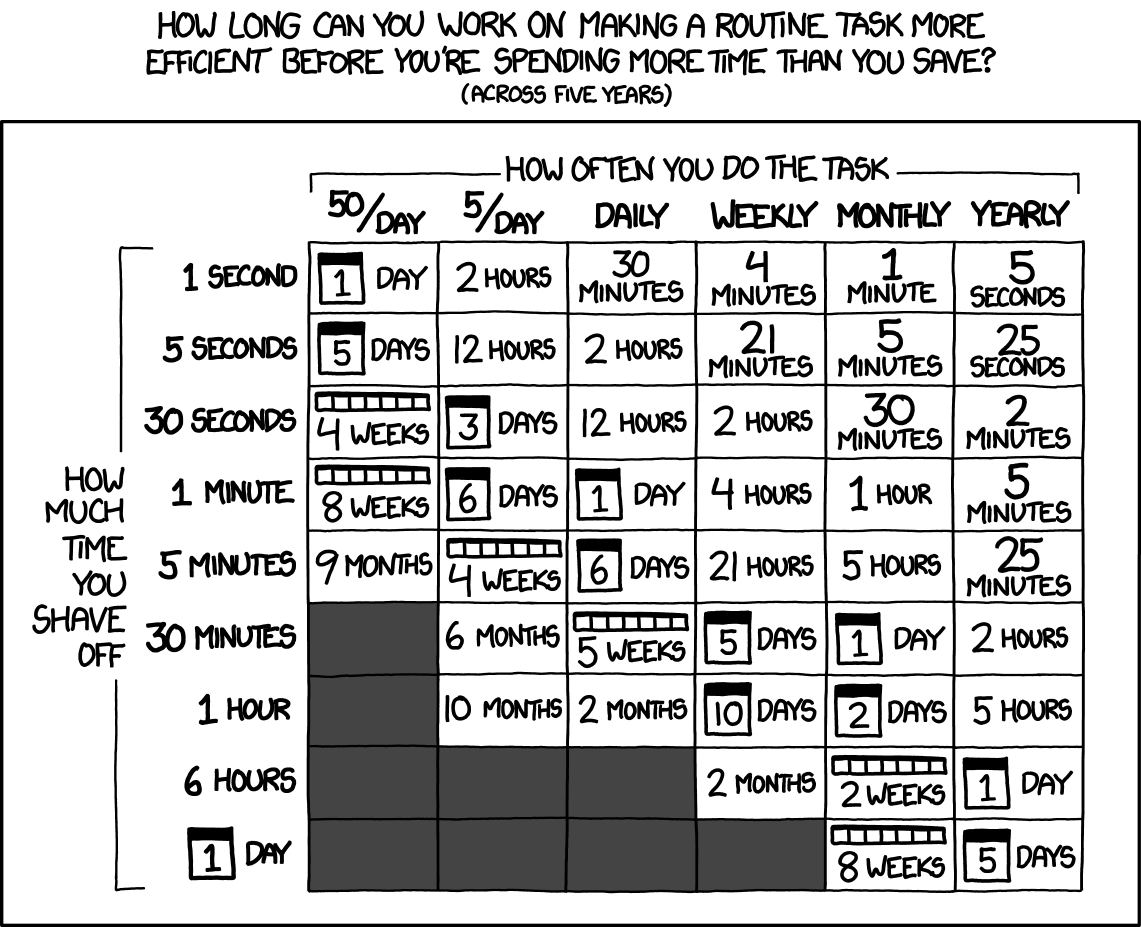
If you really really want to do it anyway#
Write tests
Profile before optimizing
Writing tests is important to keep the code running and making sure that it works the same way after optimizing. At the very least, keep a copy of the non-optimized code and test your optimized code against it.
Profiling helps to focus on what really matters. You might find the results of profiling very surprising!
Some optimisation stories from the class#
vectorization instead of for-loops
conversion between xarray/numpy arrays etc. is expensive - avoid it if you need performance
writing functions instead of hard-coding every single step multiple times
opening the same file every time in a for-loop instead of doing it once before starting the for-loop
think of writing your own functions for routines you are using a lot instead of potentially slow package functions (e.g.
np.average). See examples below.
Profiling code#
with graphics: benfred/py-spy
Optimisation examples#
Important
Always follow the further rules of scientific code optimisation in order:
Don’t do it.
Don’t do it (yet)
Test before doing it
Profile before doing it
Check vectorization (removing
forloops)Remove pandas / xarray overlay
Optimize numpy code
Check numba or PyPy
Use multiprocessing
Vectorization is awesome#
This is ALWAYS what you should check first: can you replace a for loop with numpy only arithmetics?
import numpy as np
# Derivation naive
a = np.arange(12)**2
deriv = np.zeros(len(a))
for i in range(len(a)):
if i == 0 or i == len(a) - 1:
continue
deriv[i] = (a[i+1] - a[i-1]) / 2
deriv
array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18., 20., 0.])
# Derivation vectorized
a = np.arange(12)**2
deriv = np.zeros(len(a))
deriv[1:-1] = (a[2:] - a[:-2]) / 2
deriv
array([ 0., 2., 4., 6., 8., 10., 12., 14., 16., 18., 20., 0.])
Concrete example: salem and MetPy’s interp_1d function (useful for interpolating model levels):
Back to basics: xarray -> numpy -> own functions#
Because of the “generalization overhead” (certain numpy and xarray functions are slow because they are meant to be general and do a lot of input checks.
If you know what your input looks like and have control over it, you can speed-up operations quite a bit.
xarray and pandas are slow on arithmetics#
import pandas as pd
df = pd.DataFrame()
df['data'] = np.ones(10000)
%timeit df**2
21.5 μs ± 144 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
%timeit df.values**2
3.27 μs ± 51.3 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
import xarray as xr
import numpy as np
da = xr.DataArray(np.random.uniform(size=(240, 300)))
%timeit da**2
25.4 μs ± 2.23 μs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
%timeit da.data**2
13.5 μs ± 50.8 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
Question to class: why?
numpy’s general functions are sometimes slower than the direct arithmetic solution#
d = np.arange(1, 1000)
w = d + 2
%timeit np.average(d, weights=w)
11.2 μs ± 25.3 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
def my_avg(d, wgt):
return (d * wgt).sum() / wgt.sum()
np.testing.assert_allclose(np.average(d, weights=w), my_avg(d, w))
%timeit my_avg(d, w)
3.7 μs ± 22.1 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
Question to class: why?
See also (similar story): numpy/numpy#14281
As for ALL cases of optimisation: please be aware of the risks! Make a careful gain / costs analysis.
Array creation is costly#
%timeit np.ones(1000)
1.11 μs ± 7.88 ns per loop (mean ± std. dev. of 7 runs, 1,000,000 loops each)
%timeit np.empty(1000)
177 ns ± 0.929 ns per loop (mean ± std. dev. of 7 runs, 10,000,000 loops each)
dx = 100
nx = 200
surface_h = np.linspace(3000, 1000, nx)
def grad_np(surface_h, dx):
"""Numpy computing a gradient"""
gradient = np.gradient(surface_h, dx)
gradient[[-1, 0]] = 0
return gradient
def my_grad(surface_h, dx):
"""Same result, not using numpy's function"""
gradient = np.empty(surface_h.shape)
gradient[1:nx-1] = (surface_h[2:] - surface_h[:nx-2])/(2*dx)
gradient[[-1, 0]] = 0
return gradient
def my_other_grad(surface_h, dx):
"""Same as above, but no array creation and using concatenate"""
internal_grad = (surface_h[2:] - surface_h[:nx-2])/(2*dx)
return np.concatenate([[0], internal_grad, [0]])
np.testing.assert_allclose(grad_np(surface_h, dx), my_grad(surface_h, dx))
np.testing.assert_allclose(grad_np(surface_h, dx), my_other_grad(surface_h, dx))
%timeit grad_np(surface_h, dx)
10.1 μs ± 411 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
%timeit my_grad(surface_h, dx)
3.55 μs ± 38.1 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
%timeit my_other_grad(surface_h, dx)
3.65 μs ± 26.7 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
Can we make it even faster? Put array creation outside of the function (optimization only available when a for loop is involved):
gradient_container = np.zeros(surface_h.shape)
def my_super_grad(surface_h, dx):
gradient_container[1:nx-1] = (surface_h[2:] - surface_h[:nx-2])/(2*dx)
return gradient_container
np.testing.assert_allclose(grad_np(surface_h, dx), my_super_grad(surface_h, dx))
%timeit my_super_grad(surface_h, dx)
2.28 μs ± 11.3 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
But numpy is already super clever#
The following codes do the same. It is tempting to think that the second or third examples are faster (because they use in-place operations), but it turns out that they are all exactly the same speed (within errors):
def some_calc(surface_h):
out = surface_h + 1
out = surface_h * out
out = out - 100
out = out**2
return out
def not_useful_optim(surface_h):
return (surface_h * (surface_h + 1) - 100)**2
np.testing.assert_allclose(some_calc(surface_h), not_useful_optim(surface_h))
def also_not_useful_optim(surface_h):
out = surface_h + 1
out *= surface_h
out -= 100
return out**2
np.testing.assert_allclose(some_calc(surface_h), also_not_useful_optim(surface_h))
%timeit some_calc(surface_h)
3.42 μs ± 23.5 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
%timeit not_useful_optim(surface_h)
3.42 μs ± 9.19 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
%timeit also_not_useful_optim(surface_h)
3.28 μs ± 16.9 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)
This is because python + numpy already knows how to compile this code to be optimized, i.e. it recognizes where the culprits are and solves them.
Just in time compilation#
For pure numpy code with unavoidable loops (typical for numerical models with a time stepping for example), numba is probably the best shot you have at considerably speeding up your code. We’ll make an example in class.
Numba is extensively used in some applications, e.g. for cosipy. It has some drawbacks though (we discuss in class).
For some applications, pypy might be worth a shot but it requires using another python interpreter.

